RPL Value Model

⚠️ Disclaimer. I am a Rocketpool node operator, I therefore own RPL collatoral and would benefit from its price appreciation.

Note: I do not use the terms “value” and “price” interchangeably. Value is the expected clearing price of non-speculative demand & supply. Price is what we get in the real world markets with speculators moving price above or below value.

In this article I will try to present evidence that RPL is unlikely to sustain a high value long term, even if the Rocketpool protocol is successful. To do so, I will present the following points:

1) Existing node operators are not a source of continual demand liquidity

2) The primary non-speculative demand for RPL is tied to the first derivative of protocol adoption (ie demand is tied to growth rate)

3) Growth rate is terminally sub-linear

Existing Node Operators Are Not Value

First a reminder how RPL is used. To create a new minipool, a node operator must post collateral in the form of RPL. At the time the minipool is created, that collateral must be valued at 10% of the borrowed 16 ETH (ie 1.6 ETH worth of RPL must be posted). Over time a node operator’s collateral percentage will change (as the RPL/ETH ratio changes), both to the upside and downside. If RPL’s value suddenly drops (in ETH terms) then node operators may find themselves below the 10% collateral threshold. There is nothing that forces the operator to post more collateral; the operator will still receive all ethereum-related rewards (beacon chain, commissions, MEV, & tips)

However, there does exist one incentive mechanism designed to reward over-threshold nodes at the expense of those who are under-threshold: the protocol inflates the RPL supply to deliver a yield to all node operators who are above the 10% threshold. Put another way, there is a transfer payment from all holders of RPL (including node operators who collatoralize less than 10%), to the node operators who collatoralize more than 10%. Importantly, the “punishment” for being under-threshold is constant (the inflation rate), while the “reward” for being over-threshold is dynamic depending on the ratio of under:over collatoralized nodes. This has the effect of making some eye-popping yield numbers as fewer and fewer nodes are over-threshold, in an attempt to encourage more node operators to “top up” their collatoral posting.

There is plenty of emperical evidence to show that such “ponzinomics” does in fact induce some level of demand. How much? This depends on how risky the asset is perceived to be. A higher yield is required to convince people to buy in to a more risky asset. Notably, as the risk goes to infinity, so does the required inflation to induce demand. This is why a sudden risk shock can spontaneously cause these types of assets to implode (see LUNA).

Am I saying that RPL is at risk of imploding? No, not at all; RPL does have real non-ponzi demand (see next section). The point I’m making here is that existing node operators are no different from regular speculators, and the fact that they can additionally receive some inflation-based yield is irrelevant. They will only buy more RPL if they are bullish enough on the asset to justify the risk implied by the current yield.

Node Operator Net Growth Rate Is Value

Rocketpool offers a node operation experience that has real benefits:

• You can operate a node with less than 32 ETH
• You can collect a 15% commission for staking other people’s ETH
• You can benefit from the Smoothing Pool

I believe this product has real demand (after all, I run a rocketpool node!), and the requirement to purchase 1.6 ETH worth of RPL as payment for access to this product therefore introduces real demand for the token.

On the other hand, when a node exits and has its RPL unlocked, the supply of the token is increased. If the ex-node operator chooses to hold the RPL despite not receiving benefits from it any longer, they are purely a speculator. Because I don’t include speculation as real demand, any time a node exits is negative value, regardless of if the unlocked RPL is sold and translates into a real price reduction or not.

The net of these two forces is net growth of the validator set, or put another way, the first derivative of the validator count.

Derivative Thinking

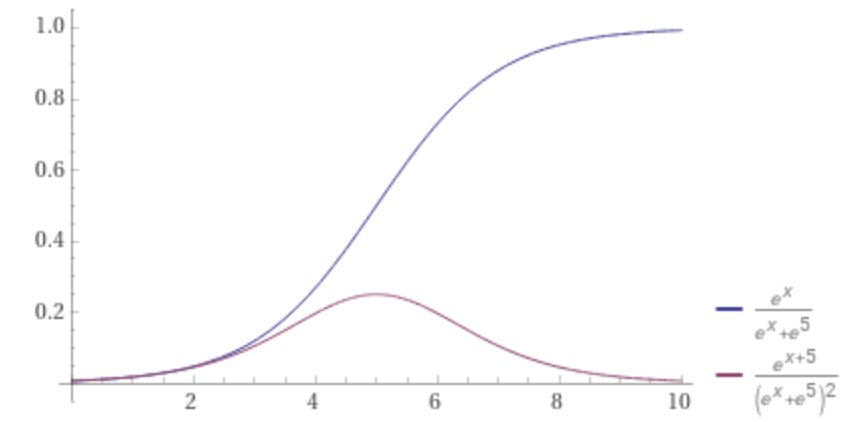
Note: The graphs in this section are poorly labelled (sorry!). The blue line is validator count over time. The purple line is RPL value over time.

If the rocketpool protocol is undergoing exponential growth, or even just high polynomial growth, then value may look like its directly correlated to the absolute number of validators.

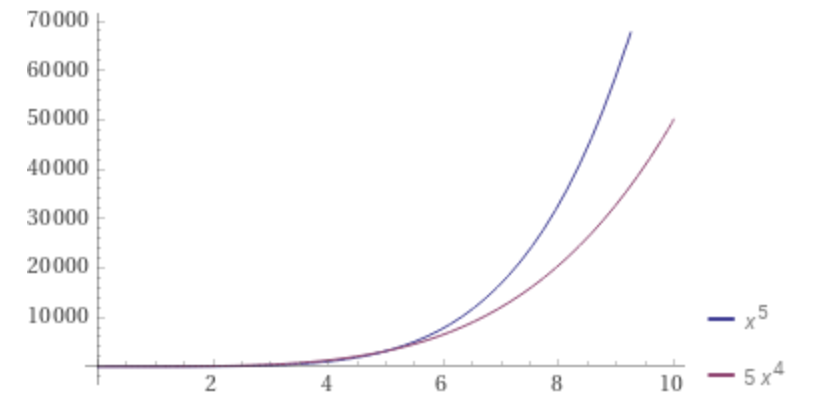
Only once growth is quadratic, does the difference between these plots start to become more apparent. If validator growth is linear, then there’s no change in value over time at all!

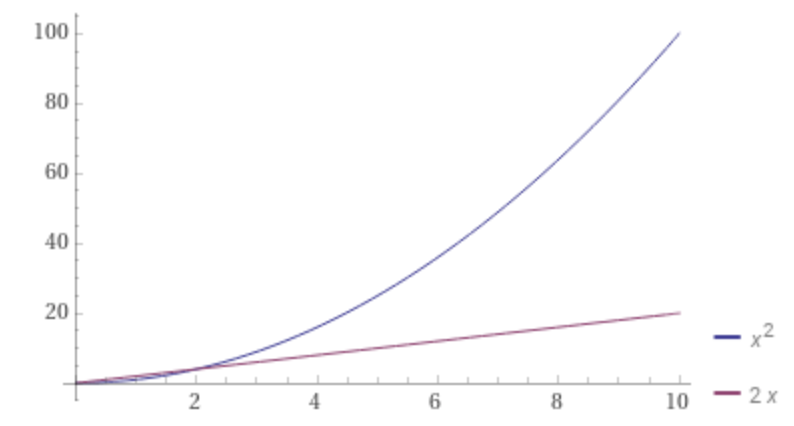
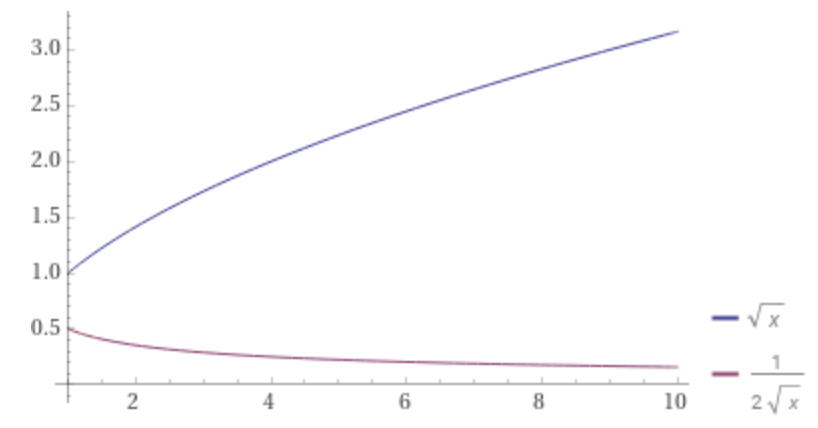
The most important realization here is that while a sub-linear growth rate does mean validator count is increasing, the first derivative is decreasing!

The Growth S-Curve

Product 101: growth can’t accelerate forever. There’s always a total addressable market that will eventually be saturated. Instead, growth tends to follow a sigmoidal curve (S-curve) with a period of acceleration followed by a period of tapering.

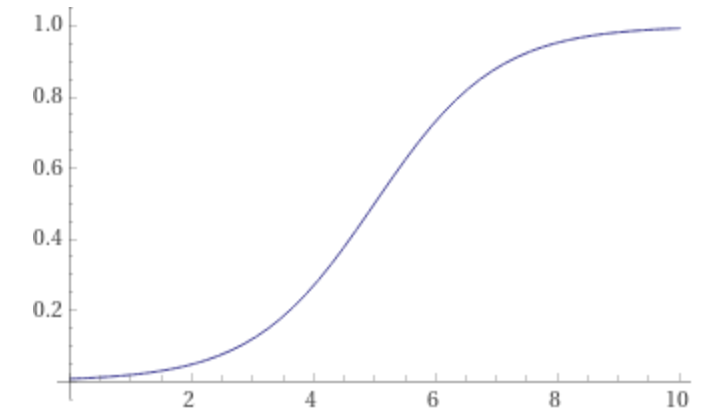
Notice that while the second half of an S-curve is still increasing in absolute value, it is sub-linear (decelerating)! It is for this reason that I expect the value of RPL to increase rapidly while Rocketpool is growing, but also expect the value of RPL to decrease rapidly while Rocketpool matures.

Value is not Price

To re-iterate one last time, the “value” of something does not mean the actual market price will follow. The power of speculation can put enormous premiums above value (just look at $DOGE). Whether these types of assets are investable really comes down to your individual strategy and risk tolerances. I’m personally a more conservative, value investor than most in the crypto-sphere, and for that reason I personally do not plan to hold RPL long-term.