Work vs Stake Profit Functions

There are many trade-offs between Proof of Work and Proof of Stake, but one that I don’t see discussed very often is how Proof of Work uniquely has a profit-based incentive to limit the centralization of the concensus layer. PoW miners begin to lose profit if they contribute too large a percentage of the hashrate, while PoS validators will generally have no problem growing as large as possible. To be clear, in this article I am only discussing this one incentive structure and it does not mean that PoW will always be more decentralized. There are many other systemic incentives at play, including the fact that the profit-based feedback loop discussed in this article is rather weak.

The Big Picture

There is a fundamental difference between the topology of these two profit functions. The PoW function has a peak at which it no longer makes economical sense to expand their operation, while the PoS function continues to increase the more stake that is added.

The below graph is the expected profit per block (every 10 minutes) for a PoW miner’s hashrate. This particular plot assumes:

• Block reward is $128,075
• Total existing hashrate is 250,000,000 TH/s
• The miner is using S19j Pro’s (30.5 W per TH/s)
• The miner’s electricity cost is 0.05c per kWh

As we can see, for this miner’s particular situation (and of course this will vary by miner) they are incentivized to grow no larger than 28% of the total network.

We can do the same plot for a PoS validator’s profit per stake. The assumptions for this plot don’t really matter; it will always be linear:

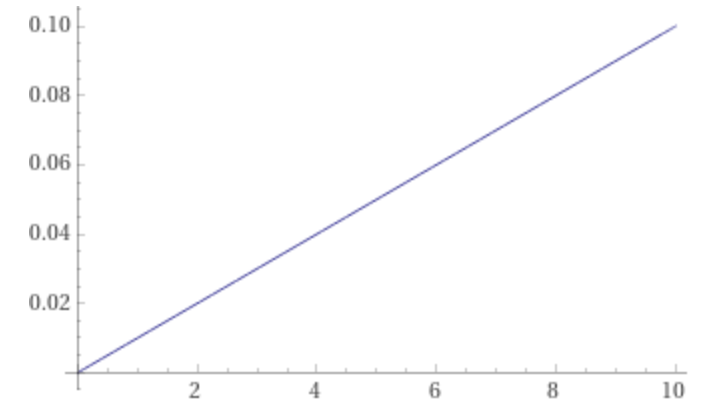
Below is the reasoning and equations for these plots.

Proof of Work Profit

Revenue under PoW is simply the percentage of global hashrate provided multiplied by the block reward:

\[R = B * {h \over H + h}\]

where

• \(B\) is the block reward
• \(h\) is the miner’s hashrate
• \(H\) is the global hashrate

PoW miner also have some fixed costs (real estate) and some marginal cost per hash (ie electricity)

\[C = c_f + c_m * h\]

where

• \(c_f\) is the fixed costs
• \(c_m\) is the cost per hash
• \(h\) is again the miner’s hashrate

Overall, we arrive with a profit function of the form:

\[P = B * {h \over H} - c_f - c_m * h\]

Proof of Stake Profit

Revenue under PoS is similar to that of PoW: the validator’s percentage of global stake multiplied by the block reward (note that “block reward” in this context includes averaging proposals, attestations, mev, tips, and possibly commissions over time)

\[R = B * {s \over S}\]

where

• \(B\) is the block reward
• \(s\) is the validator’s stake
• \(S\) is the global stake

PoS validators will have some fixed costs (real estate), but effectively no “cost per stake” (we don’t include “opportunity cost” as a cost)

\[C = c_f\]

where

• \(c_f\) is the fixed costs

Overall, we arrive with a profit function of the form:

\[P = B * {s \over S} - c_f \]

Why no opportunity cost?

Opportunity cost is a useful tool for making decisions, but I don’t consider this to be a real operating cost. The reason is risk. Sure, running an Ethereum validator “only” yields 5%, but anything that would has the potential to return more is also higher risk. Each unit of capital has its own risk tolerance. If I’m trying to allocate a portion of my capital that is only comfortable with the risk profile of a 5% potential return, there is no opportunity cost to deploying a validator. Deploying this capital to a higher risk asset is not an option